데이터표기
리터럴
데이터-> 전기신호(정수, 부동소수점)
데이터 표기
| 문자열(문자개수+a) | "홍길동" | " ": 빈 문자열 가능 / 문법오류: '홍길동 |
| 문자(2byte) | '홍' | 문법오류: '홍길동' |
| 숫자 | 정수 | 4byte | 10 |
| 8byte | 10L, 10l | ||
| 부동소수점 | 4byte | 10f / 10.2f, 3.14f | |
| 8byte | 10.2 / 10.2D, 10.2d (보통 d 생략) | ||
| 논리 | true, false (4byte), 배열인 경우 1byte 사용 | |
| 레퍼런스(주소) | 표기할 수 없다 | |

정수리터럴
| 78 | 10진수 |
| 0116 | 8진수 |
| 0x4E | 16진수 |
| 0X4E | |
| 1B01101110 | 2진수 (B 앞이 0이면 양수, 1이면 음수) |
| 0B01101110 |
부동소수점 리터럴
(소수점이 둥둥 떠다닌다.. floating point.. 부상의 부)
| 3.14 (일반 표기법) | |
| 31.4E-1 (= 31.4e-1) | 31.4 x 10^-1 |
| 314E-2 | 314 x 10^-2 |
| 0.314E1 | 0.314 x 10^1 |
| 0.0314E2 | 0.0314 x 10^2 |
문자리터럴
| '가' '\uAC00' '\uau00' \u : escape character 탈출명령..! |
| 'A' '\u0041' '\041' 유니코드 |
| "\uAC00나다" = "가나다" => 문자열 안에 유니코드 표기법을 사용할 수 있다. |
데이터 -> 전기신호 : 정수
1. sign-magnitude 방식 (부호 절대 값 방식) : 부동소수점의 가수부 값을 저장할 때
0과 -0이 존재하며, 덧셈 뺄셈 처리하는 별도 회로가 필요하여 하드웨어가 복잡해짐
사람이 이해하기는 쉬움
2. ones complement : 1의 보수
1의 보수는 이진수를 뒤집는 역할
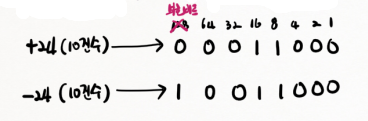
| +24 => 00011000 | 양수값은 그대로 2진수로 변경 |
| -24 => 11100111 | 1의 보수로 음수 저장 |

3. 2의 보수
=>현대 컴퓨터는 2의 보수 방식으로 정수를 다룬다.
=> 1의 보수 값에,, 미리 1을 더한다!

1 + (-1) = 0
1. -1을 1의 보수 값으로 구하고 +1 한다.
2. 1의 이진수 값 + 1 하면 ...
3. 0
4. Excess -k (k 초과)
"원래의 정수 + k 값" 을 이진수로 바꾼 값
=> 부동소수점을 계산하는 방식


데이터 -> 전기신호 : 부동소수점
(32bit : 부호비트(1) + 지수부(8) + 가수부(23) )
(64bit : 부호비트(1) + 지수부(11) + 가수부(52) )
12.375
1. 12를 표현가능한 비트로 표현: 1100
2. 0.375 계산
| 0.375 x 2 = 0.75 = 0 0.75 x 2 = 1.5 = 1 0.5 x 2 = 1.0 = 1 => 0.011 |
3. 1100 + 0.011 = > 100.011
4. 정규화 : 소수점 왼쪽에 한개의 1만 남도록 변경
=> 1.100011 x 2^3
5.
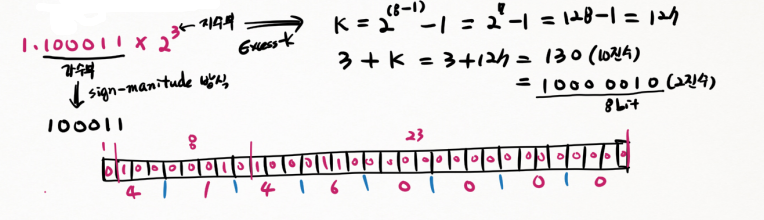
6. 값: 41 46
final float f = 12.375f; 컴파일: 41 46
final double d = 12.375; 컴파일: 40 28 c0 00 00 00
ChatGPT
부동 소수점은 IEEE 754 표준에 따라 표현되며, 이 표준은 32비트 float와 64비트 double의 부동 소수점 형식을 정의합니다.
12.375f는 32비트 float 형식으로 표현되므로, 32비트를 16진수로 표현하면 8자리가 됩니다.
따라서 "41 46"은 32비트 float로 표현된 12.375의 16진수 표기입니다.
반면, 12.375은 64비트 double 형식으로 표현되므로, 64비트를 16진수로 표현하면 16자리가 됩니다.
"40 28 c0 00 00 00"은 64비트 double로 표현된 12.375의 16진수 표기입니다.
이러한 16진수 표기는 숫자를 메모리에서의 비트 패턴으로 나타낸 것입니다. 각각의 16진수 값은 4비트를 나타내며, 두 개의 16진수 값이 결합되어 하나의 바이트를 나타냅니다. 따라서 32비트 float는 8자리의 16진수 값으로, 64비트 double은 16자리의 16진수 값으로 표현됩니다.
이러한 표기법은 숫자를 메모리에서 저장하고 전송하는 데 사용되며, 숫자의 정밀도와 범위를 효율적으로 표현할 수 있도록 도와줍니다.
'[네이버클라우드] 클라우드 기반의 개발자 과정 7기 > 웹프로그래밍' 카테고리의 다른 글
| [NC7기-24일차(5월26일)] - 웹프로그래밍 5일차 (5) | 2023.05.26 |
|---|---|
| 충격적인 숫자 리터럴 (0) | 2023.05.25 |
| 5/25 깃 사용법, gradle (0) | 2023.05.25 |
| [NC7기-22일차(5월24일)] - 웹프로그래밍 3일차 (0) | 2023.05.24 |
| 5/24 git, gradle (1) | 2023.05.24 |